POEMA PARA EL DÍA ESCOLAR DE LAS MATEMÁTICAS. 12 DE MAYO

El heroinómano en un portal que bajo una manta se asoma
al espejo de papel de plata donde se arroja Narciso y

entre estas cuatro paredes
el deseo
teniendo un horizonte
mientras añado desorden
al desorden de tu entraña y

en la tele: el 2-el 6-el 0-el 1-el 2-el 9...


En un espacio hiperbólico por un punto
exterior a una recta discurren
infinitas paralelas

DATOS DEL POETA: Javier Moreno (Murcia, 1972) aparece en la Primera Antología de Poesía con Matemáticas, de la editorial Amargord, al que pertenece el texto anterior.  No es extraño, por tanto que haya cursado estudios de Matemáticas y de Teoría de la literatura y literatura comparada. Como poeta, destacamos Cortes publicitarios (galardonado con el Premio Nacional de Poesía Fundación Cultural Miguel Hernández, ed. Devenir, 2006), Acabado en diamante (Premio Internacional de Poesía Joven La Garúa, La Garúa, 2009) y Renacimiento (Icaria, 2009). Ha aparecido antologado también en La luz Nueva. Singularidades en la narrativa española actual (Berenice, 2007),  Mejorando lo presente. Poesía española última: postmodernidad, humanismo y redes (Caballo de Troya, 2010), Pequeñas resistencias V (Páginas de Espuma, 2010), Mi madre es un pez (Libros del silencio, 2011) y Döppelganger (Jekyll&Jill, 2011). Pero también es novelista (Buscando Batería (Bartleby, 1999), La Hermogeníada (Aladeriva, 2006), Click (Candaya, 2008), Alma (Lengua de Trapo, 2011)) y dramaturgo.

Algunos enlaces sobre él:
https://peripatetismos2.blogspot.com/

COMENTARIO: "Si un verso considerado bien equilibrado le quitas o añades una palabra, lo inutilizas. Si a una ecuación -que no sea un desarrollo de términos aproximativos-, le quitas o le añades un término, también la inutilizas", dice el poeta Fernández Mallo, uno de los representante de lo que se ha dado en llamar postpoesía. Y algo de cierto debe contener esa posición, porque los poemas se construyen con las palabras adecuadas, en una estructura determinada y cuya relación debe ser exacta. Por consiguiente, siempre tenemos un criterio para saber, por ejemplo, si un poema está completamente terminado o si es consistente, solo basta con intentar cambiar algo en él: o la estructura o las palabras. Si admite cambios, algo falla, aunque parezca que se aproxima a la certeza. Por cosas así, la poesía y la matemática tienen mucho que compartir, y tiene sentido dedicar una entrada a esta efeméride que se celebra esta semana en todos los centros educativos.

Las matemáticas y la poesía tienen una relación fructífera, pero como todo aquello que merece la pena, hay que buscarlo con detenimiento y no es fácil comprender dicha relación. En este mundo de posibilidades, he encontrado poemas maravillosos y poetas que intentan renovar el lenguaje desde la ciencia en general y la matemática en particular. (La poesía fractal, por ejemplo, del esquivo Ramon Dachs, me resulta tan enriquecedora como las propuestas de OuLiPo y merecen una entrada específica en este blog). No se trata de incorporar lenguaje científico como una estratagema del poeta. El propio Moreno lo explica así: "No hacer un poema sobre el número pi -por ejemplo-, sino que ese poema constituya una metáfora de dicho número". 

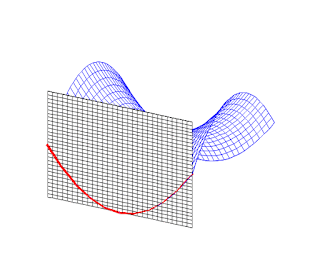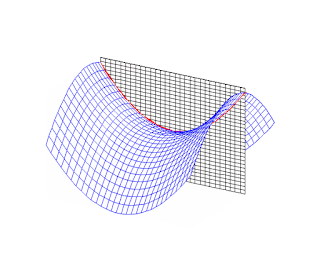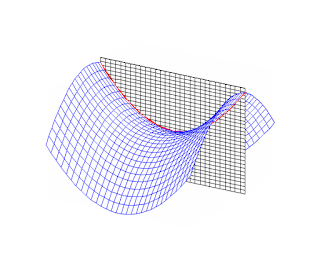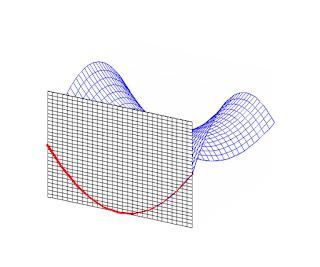
Su propuesta poética funciona, porque, de hecho, el poema explica la definición que aparece al final. Ahí radica su virtud. Cualquier neófito que odie las matemáticas y no quiera saber nada de su lenguaje, entiende el poema y, por inclusión, como funcionan parcialmente las posiciones relativas de dos rectas del Plano Hiperbólico. En el caso que nos ocupa, son dos rectas ultraparalelas, es decir, son disjuntas incluso en sus prolongaciones hasta la recta del infinito. 

(Plano Hiperbólico,

Fuente: http://www.mat.ufpb.br/lenimar/animacoes.htm)

No es nada fácil comprender lo anterior (disjuntas,  rectas ultraparalelas, plano hiperbólico, etc.), sobre todo, porque se trata de matemáticas no euclidianas. Es decir, matemáticas que no son las "clásicas" que estudiamos en la escuela. Son matemáticas que, por ejemplo, en geometría resultan más difíciles de visualizar, ya que si nos remitimos a Euclides, y desde Tales, la suma de los triángulos suma 180º; pero en la geometría hiperbólica, la suma es menor de 180º... Para entender esto, hace falta estudiar matemáticas no euclidianas como las del matemático húngaro János Bolyai o el ruso Nikolai Ivanovich Lobachevsky.  

Y, sin embargo, al leer el poema ocurre algo curioso, ya que Moreno nos ayuda a vislumbrar algo nuevo. Bajo mi punto de vista, el drogadicto a la heroína sintiendo el vértigo de un Narciso moderno al reconocer su dependencia; el amante en la antesala del deseo; y el pobre que sigue el sorteo esperando que la suerte le sonría de una vez por todas para cambiar su destino, forman parte de la misma realidad. Comparten ese mismo plano hiperbólico de realidad, ese anhelo por ser otro, por vivir una vida más auténtica y más plena y tal vez, imposible y que se nos escapará siempre. No como historias paralelas que no se cruzarán nunca, que no se tocan como en Euclides, sino más bien todo lo contrario: mostrando que esas vidas tan distintas, forman parte de una misma realidad que se repite hasta el infinito, pero que se tocan en un punto determinado. En este caso, el propio poema valdría para verificar la hipótesis.

Explicación de qué son las rectas ultraparalelas en 

el Plano Hiperbólico (Fuente: Ujué Rodríguez "Herramientas hiperbólicas

y proyectivas en Geogebra", aquí)

Ahora, gracias al acierto del poeta, gracias a su magnífico poema, entendemos un poco el postulado final, esa definición que, como una especie de barbarismo, cobra cierto sentido lírico y demuestra el poder persuasivo de la matemática al hacer poesía con matemáticas. Con esa intención escribe Moreno y ese es su gran acierto. La matemática tiene pleno derecho a estar en un blog de poesía: ambas explican lo que somos.

ACTIVIDADES:

• Desde el blog EL POEMA DE LA SEMANA podéis encontrar poemas para esta efeméride. Os dejo algunas entradas:

EJERCICIO NÚMERO 1 (PROBABILIDAD)

MATEMÁTICAS FUERA DEL TIEMPO

EL SONETO MATEMÁTICO

TOPOLOGÍA DE UNA PÁGINA EN BLANCO

IMAGINA SI SOMOS DOS

LAS HUELLAS

• Busca que es la postpoesía, en este blog le dedicamos hace tiempo una entrada. ¿Qué te parecen sus postulados?
• Busca información sobre la contribución de János Bolyai y Nikolai Ivanovich Lobachevsky a las matemáticas. ¿Para qué sirve las matemáticas no euclidianas?
• Creemos que con las matemáticas, los números y el azar se pueden plantear múltiples actividades en el aula. Ahora te proponemos una que se llama: BINGO Y ESCRITURA. ¿Os atrevéis a jugar...? Pincha aquí para conocer la actividad. Y aquí si quieres ver un ejemplo de la puesta en práctica.
• 
• (O aquí)
  

En el Comentario se habla de lo importante de la estructura de un poema. Basándonos en esa idea, podemos realizar las siguientes actividades para reescribir poemas.

(Pincha para ampliar o pincha aquí)

(Pincha para ampliar o pincha aquí)

• Busca información aquí sobre el Día Escolar de las Matemáticas, pincha aquí. Busca información sobre Pedro Puig Adam, ¿cómo te imaginas su vida?, ¿te parece adecuado elegir este día en su honor? Justifica tu postura.
• Existe un cuaderno del Día Escolar de las Matemáticas, este año dedicado a los mapas. Lo puedes descargar, en pdf, en el siguiente enlace: https://revistasuma.es/IMG/pdf/dem2019-3.pdf  El cuaderno, así como el resto de actividades han sido elaboradas por Raúl Ibáñez, doctor en Matemáticas por la Universidad del País Vasco. 
• Intenta realizar barbarismos con términos matemáticos de la matemática clásica o euclidiana y con conceptos matemáticos de la no euclidiana. Para ello, lee esta actividad:

(Pincha para ampliar o pincha aquí)

• ¿Crees que la poesía y la matemática sirven para conocernos a nosotros mismos? Razona tu respuesta.
• Deja un comentario en este blog, puedes contar tu relación con las matemáticas que, seguro, tienen mucho de poético o drama o comedia.